The paper introduces a novel mechanism to bring about improvements to the task of sequence to sequence modelling. I think it's worth taking a minute to really drill down on the setup, the problem and then delve into how anttention is gonna solve that problem. The complete implementation of the paper is available here. Since I want to focus on attention I'm gonna be using a subset of the code here.
If you're not aware of how an RNN functions you need to stop here understand that first. I think Andrej Karpathy's blogpost is a brilliant place to understand RNNs from the ground up.
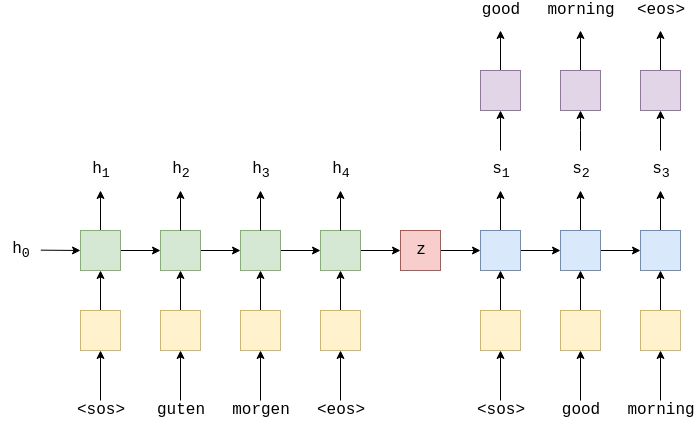
A hidden state is a vector of fixed size representing a sequence. So, from the diagram h3 represents the sequence till morgen.
The seq-to-seq setup is usually used for machine translation. So, the last hidden state which represents the entire sequence becomes the initial hidden state for another RNN that is going to output the translated sequence.
This is the basic setup for a seq-to-seq model. Now, let's take a look at the paper describing the problem with this steup.
Most of the proposed neural machine translation models belong to a family of encoder–decoders, with an encoder and a decoder for each language, or involve a language-specific encoder applied to each sentence whose outputs are then compared. An encoder neural network reads and encodes a source sen-tence into a fixed-length vector. A decoder then outputs a translation from the encoded vector. The whole encoder–decoder system, which consists of the encoder and the decoder for a language pair,is jointly trained to maximize the probability of a correct translation given a source sentence.
A potential issue with this encoder–decoder approach is that a neural network needs to be able to compress all the necessary information of a source sentence into a fixed-length vector. This may make it difficult for the neural network to cope with long sentences, especially those that are longer than the sentences in the training corpus. Choet al.(2014b) showed that indeed the performance of a basic encoder–decoder deteriorates rapidly as the length of an input sentence increases.
I want highlight what I feel is the important part of this description:
A potential issue with this encoder–decoder approach is that a neural network needs to be able to compress all the necessary information of a source sentence into a fixed-length vector.
To tackle this, this paper has developed a mechanism which allows us to fetch information from different segments of the input sequence for each prediction we make.
Enter: Anttention
When we're using anttention, the first input that the decoder recieves is the < start > token and a fixed length vector which contains information weighted towards the segment we want to translate. (Let's keep this statement in mind which become clearer with code) for the translation. Let's call this vector the context vector.
The context vector will be created from the list of hidden states from the encoder.
Here, I would say we're ready to look at how the anttention mechanism functions as we have descibed in plenty detail the two inputs anttention requires:
- A list of vectors from which I want to extract some information.
- A vector which is gonna help me gauage what information I want to extract.
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
ENC_HID_DIM = 512
DEC_HID_DIM = 512
attn = nn.Linear((ENC_HID_DIM * 2) + DEC_HID_DIM, DEC_HID_DIM)
v = nn.Linear(DEC_HID_DIM, 1, bias = False)
Here I'm going to create an artifical torch vectors to step through the mechanism. I would encourage you to go through the complete implementation of the paper once you're done here. I am attaching a notebook which as the complete implementation. (Here onwards follow along the comments as I'm explaning what's hapening in the comments)
# In the first step, this is gonna be the last hidden state passed through a linear layer.
# Shape: (batch_size,decoder_hidden_dimension)
# batch_size: Num of sequences we're processing
# decoder_hidden_dimension: hidden state dimension of the decoder RNN
hidden = torch.randn(1,512)
# List of vectors (Encoder Outputs)
# Here the shape is (src_len,batch_size,encoder_hidden_dimension)
# src_len: Length of the source sequence
# batch_size: number of sequences I'm processing in one go
# encoder_hidden_dimension: size of the hidden states in the encoder
encoder_outputs = torch.randn(5, 1, 1024)
# I have taken this code from the `forward` method of
# the anttention class. I'm going to be printing the
# dimensions/ values of vaiables to keep track of what's
# happening
batch_size = encoder_outputs.shape[1]
src_len = encoder_outputs.shape[0]
print(batch_size)
print(src_len)
# and each encoder outputs. I want to see how much
# information does each vector contain which will help
# me predict the next output. Thus, to perform such an
# operation I'm creating duplicates of the last hidden state for each encoder output.
#repeat decoder hidden state src_len times
print(hidden.shape)
hidden = hidden.unsqueeze(1).repeat(1, src_len, 1)
print(hidden.shape)
print(encoder_outputs.shape)
encoder_outputs = encoder_outputs.permute(1, 0, 2)
print(encoder_outputs.shape)
Referencing the paper, the following three operations are represented by the following operation in the paper:
$$e_{ij} = a(s_{i-1},h_i)$$
In the expression, we're calculating a score for each encoder output.
# vector and every encoder output vector.
print(hidden.shape)
print(encoder_outputs.shape)
concat_hidden_encoder = torch.cat((hidden, encoder_outputs), dim = 2)
print(concat_hidden_encoder.shape)
# vectors of size 1536 to 512. Simple Matix Multiplication.
energy = torch.tanh(attn(concat_hidden_encoder))
print(energy.shape)
v(energy).shape
attention = v(energy).squeeze(2)
print(attention.shape)
In the paper the softmax in the following cell is represented as:
$$\alpha_{ij} = \frac{exp(e_{ij})}{\sum_{k=1}^{T_x }exp(e_{ik})}$$
# useful each encoder output vector will be in determining the next output.
# Lastly, I want to normalize the scores. I'm gonna do this via softmax.
# This is the same softmax which is used in classification.
encoder_softmax = F.softmax(attention, dim=1)
# which sums up to 1. Here, they can be seen as weights describing the importance
# of each encoder outut vector.
encoder_softmax[0]
encoder_softmax = encoder_softmax.unsqueeze(1)
encoder_softmax.shape
# of each encoder output in determining the next output. It's found that
# when I multiply each encoder output with its weightage and add them all up
# I get the information I was looking for from the initial set of encoder outputs.
# This particular operation is in the Decoder of the Seq-to-Seq model.
weighted = torch.bmm(encoder_softmax, encoder_outputs)
encoder_outputs.shape
weighted.shape
In the paper, the weighted vector is referred to as the context vector and calculated as the follows:
$$c_i = \sum_{j=1}^{T_x }\alpha_{ij}h_j$$
class Attention(nn.Module):
def __init__(self, enc_hid_dim, dec_hid_dim):
super().__init__()
self.attn = nn.Linear((enc_hid_dim * 2) + dec_hid_dim, dec_hid_dim)
self.v = nn.Linear(dec_hid_dim, 1, bias = False)
def forward(self, hidden, encoder_outputs):
# import pdb;pdb.set_trace()
#hidden = [batch size, dec hid dim]
#encoder_outputs = [src len, batch size, enc hid dim * 2]
batch_size = encoder_outputs.shape[1]
src_len = encoder_outputs.shape[0]
#repeat decoder hidden state src_len times
hidden = hidden.unsqueeze(1).repeat(1, src_len, 1)
encoder_outputs = encoder_outputs.permute(1, 0, 2)
#hidden = [batch size, src len, dec hid dim]
#encoder_outputs = [batch size, src len, enc hid dim * 2]
energy = torch.tanh(self.attn(torch.cat((hidden, encoder_outputs), dim = 2)))
#energy = [batch size, src len, dec hid dim]
attention = self.v(energy).squeeze(2)
#attention= [batch size, src len]
return F.softmax(attention, dim=1)
Here I have tried to cover the very core of the attention mechanism. Before moving forward I would highly reccomend to go through the entire implementaton here. I have added several debuggers (pdb) in the Encoder, Decoder, Attention and the final model.
To summarise: given the input of a list of vectors L and a vector x, attention gives a weightage which signifies the dependence of the vector x on each entity in the list L.